Puzzle solutions, Issue 01

These solutions relate to puzzles found in Issue 01 of the magazine.

#2 – Circles

Call the blue area $B$ and the red area $R$. Then

\begin{align*}
R & = \mbox{Area of quarter circle} – \mbox{Area of semicircle} – (\mbox{Area of semicircle} – B)\\
& = \frac{1}{4}\pi(2r)^2 – \frac{1}{2}\pi r^2 – \left(\frac{1}{2}\pi r^2 -B\right)\\
& = \pi r^2 – \frac{1}{2}\pi r^2 – \frac{1}{2}\pi r^2 +B\\
& =0+B\\
&=B
\end{align*}

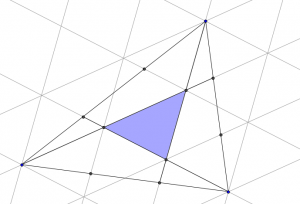
#104 – Two Triangles

Draw on the following lines parallel to those which were added in the question.

Then a grid of copies of the smaller blue triangle has been created.

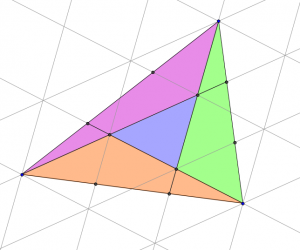
Now consider the three triangles which are coloured green, purple and orange in the following diagram:

Each of these traingles covers half a parallelogram made from four blue triangles. Therefore the area of each of these triangles is twice the area of the small blue triangle.

And so the blue triangle covers one seventh of the large triangle.