It is altogether too hot, it is altogether too full of people, and it is altogether too lunchtime for what feels like 8pm. Fortunately, the organisers have fed mathematicians before, and have thoughtfully provided plain paper tablecloths and pens with which to postulate, puzzle and prove while we eat. We’re in Atlanta, Georgia for the 13th Gathering 4 Gardner, or G4G: every couple of years, mathematicians, magicians, sceptics, jugglers and assorted others gather to honour the work and memory of popular science writer Martin Gardner with a week-long conference.
An idea from an earlier talk had lodged in my head. Cindy Lawrence of MoMath—New York’s Museum of Mathematics, where one can ride a square-wheeled tricycle or explore the inside of a Möbius strip, the kind of thing that Gardner would certainly have written about—had raved about Truchet tiles. What are they? Well, start with a square, coloured either black or white. Pick two diagonally-opposite corners and shade them with a quarter-circle of the other colour, as shown. Make several. Then place them however appeals to you! The way they’re set up, it’s practically impossible not to start making patterns: blobs and whorls that seem almost alive.
Of course, you don’t need the tiles themselves. You can just as easily doodle them on a convenient sheet of paper, such as a tablecloth. And you can just as easily start asking yourself questions like, what kinds of tiles can you get if you remove the restriction of squareness? What happens if you move into three dimensions? And is there any pretty maths underlying the pretty patterns?
Sébastian Truchet and his tiles
The tiles Lawrence talked about are not, strictly speaking, due to Truchet. In 1704, Sébastien Truchet published A Memoir On Combinations, in which he discusses squares split diagonally into triangles (pictured right), giving four possible orientations for each tile.
It’s an interesting read. Truchet methodically looks at the number of ways you can place two such tiles next to each other, edge-to-edge. (He says that he’s started work on three tiles, but isn’t happy with it yet. I’ve seen nothing to make me believe he ever was happy with it.)
In the paper, Truchet carefully reasons that there are:
- four possible orientations for a single tile;
- four positions to place a second tile next to a first (north, south,
east, or west); and
- four orientations for each of the second tiles
… making a total of 64 possible arrangements.
He then notes that some of the arrangements are indistinguishable from others: placing a tile in orientation A to the left of a tile in orientation B is the same as placing B to the right of A, reducing the number to 32. Furthermore, some arrangements are rotations of others—for example, arrangement AA (pictured below) is a rotation of arrangement CC (not pictured below unless you’re reading Chalkdust upside down).
In all, he reduces the 64 original possibilities to 10 (six appear in eight configurations each, and four—those with `stripes’ across the middle—appear four times apiece).
It turns out to be worthwhile to consider the overlying structure of these arrangements. Of the ten possibilities, eight appear in pairs: swapping the colours of one gives the other. The other two are self-inverse: swapping the colours gives a rotation of the original arrangement.
And that’s where Truchet tiles remained until the 1980s, when CS Smith, writing in Leonardo, took a deeper dive into the topology of Truchet tiles.
Among other things, he suggests several possible changes to the design—for example, removing colour from the equation altogether and simply tiling with diagonal lines, or—rather nicely—by a pair of arcs in opposite corners. This is, in terms of symmetries, just the same as a diagonal, but placing large numbers of them together makes for much more appealing patterns—which you should totally play around with, but after you’ve finished reading this article.
Smith also suggests extending these tiles to include colours: if you make the cut-off corners one colour, and the remaining strip of the tile the other, you have exactly the blobby-cornered tiles MoMath brought to G4G.
But why limit yourself to squares?
Extending tiles to 2n-gons
Don’t get me wrong, I have nothing against squares. They’re certainly in my top ten favourite shapes. Just… even if the tessellation patterns are neat, the configurations of the tiles themselves are not all that interesting. When you go beyond four sides using blobby corners and two colours, though, fascinating things begin to emerge, without even having to put the tiles next to each other. (From here on, you can assume that all tiles are blobby-cornered and two-coloured.)
Indeed, any regular polygon with an even number of sides can be turned into blobby Truchet tiles (although hexagons are the only ones that would tile the plane alone). Odd numbers of sides don’t work with this kind of colouring, because the vertices need to alternate between two colours. How many hexagonal tiles are there? Well, it depends how you count.
I choose to count rotations of the tile as the same tile—so there exactly two square tiles, one with two isolated white corners and one with two isolated black corners.
With hexagons, it’s simple enough to do the counting: let’s start by considering the three white corners and how they connect (or don’t connect) to each other. Either each corner is on its own, all three are connected, or a pair of corners is connected and the other isolated. (Note that if any member of a group of corners connects to another corner, all members of that group must connect—we can’t have a case where the first corner connects to the second and the second to the third unless the first and third are also connected.)
These correspond to the figures to the right—three isolated white corners and three interconnected white corners, followed by—more interestingly – an isolated white corner, followed by a black band that ends halfway across the hexagon, followed by a white band and an isolated black corner.
I’ve paired them like this for a very good reason: inverting the colours on the black dots tile gives the white dots, and vice versa; inverting the colours on the split hexagon gives… a rotation of itself! I count the hexagons as having three possible tiles, one of which is self-inverse.
What possible patterns are there for an octagon?
Obviously, octagons don’t tile the plane on their own (although there’s nothing to stop you filling in the gaps with square tiles!) Independent of how we’re going to arrange them, we can still consider the viable patterns.
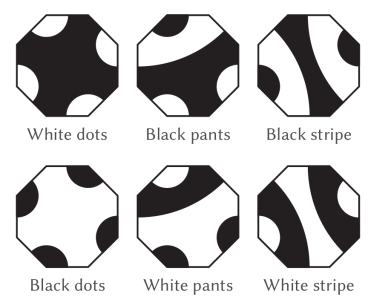Again, it’s good to start by considering the four white corners and how they connect. When none of them connect, we have another white dots pattern; when all four connect, we have a corresponding black dots pattern. These two are inverses.
If two neighbouring corners are joined, and the other two left unattached, the resulting shape looks like a pair of black pants. Its inverse pattern, the pair of white pants, arises from any three white vertices being connected.
We could also connect a pair of diagonally-opposite corners to give a white stripe; the black stripe comes from connecting one pair of adjacent vertices, then connecting the remaining pair.
The octagons therefore have six possible tiles, none of which is self-inverse. (Or do they? Have I counted correctly? How do you know?)
Decagons are where (for me) it gets interesting: but perhaps you want to try working out how many decagon tiles there are yourself first. Scroll down once you’ve had a go…
There are ten decagon tilings, up to rotation—of which two are self-inverse. That’s a structure we’ve seen before: it’s the same as the structure behind Truchet’s pairs of adjacent tiles. Don’t you think that’s neat? Well, hold my coffee.
Truchet tiles in three dimensions
The following day, I pick a table with the MoMath people, who have a set of the square blobby tiles out to play with, black with white corners one side, white with black corners on the other. “How many ways can you make a cube?” asks Tom. We pick up the tiles and try to arrange them, one per face.
Let’s adopt the reasonable rule that the corners of each tile that meet a vertex must be the same colour. Each face then has two diagonally-opposite black vertices, and two diagonally-opposite white vertices, and there are only two ways to place a blobby tile to satisfy that: either the black vertices are joined by the stripe, or the white ones are. We can therefore think of each face as either black (if its black vertices are connected), or white (if the white pair is joined).
The puzzle reduces to finding how many ways there are to colour the faces of a cube using only two colours.
If all six faces are white, there’s only one possibility. The same goes for no white faces.
If five are white, there is again only one possibility (up to rotational symmetry); this is also true for one white face.
With four white faces, there are two possibilities: either the black squares are on opposite sides, or they are on adjacent sides. As you might expect, the same goes for two white faces.
With three white faces, there are again two possibilities: either the three faces meet at a vertex, or they wrap around like a tennis ball.
Now, simply listing the possibilities isn’t all that interesting. However, the structure behind the list is: of the ten arrangements, eight have a natural colour inverse, and the other two are self-inverse – switching the colours gives you a rotation of the same cube.
That’s precisely the same as the structure of the decagonal tile arrangements—and Truchet’s original pairs.
Coincidence?
It’s not clear to me whether this repeated structure is a coincidence, or some deep property of Truchet tiles. It’s not unnatural for a ten-element set to have that same structure—two elements that are their own inverses, and eight that form inverse-pairs.
Indeed, if you consider the group of integers from 0 to 9 under addition modulo 10, you also get that structure (0 and 5 are self-inverse). However, to consider the tiles or cubes as a group, we’d need a way to combine them in pairs, and if there’s a simple operator for any of the Truchet sets, it’s not obvious to me.
So, I’m opening it up to you, knowing that the readership of Chalkdust has, collectively, far more insight than I do: is this common structure a coincidence, or something deeper?
While you’re working it out, draw some Truchet tiles of your own. You’ll be glad you did. See you later, tessellator!
