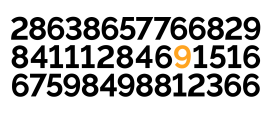May the bending and twisting forces be with Hannah Woods
Mats Vermeeren gets involved in involutes
Peter Rowlett gets in a tangle ... KNOT!
Bror Hjemgaard gets out his numerical toolbox
Donovan Young finds every connection wherever he goes.
David Budd gets carried away joining the dots. Resistance is few-tile.
Potatoes, mugs and doughnuts with Ashleigh Ratcliffe.
Matthew Scroggs explains how to get digits all riled up
Hayden Mankin combines traditional art with randomness
Calum gets on his soap box about toy models
Madeleine Hall is overwhelmed
Sara Logsdon looks to graph theory and abstract algebra for help on the puzzle page
...of three recent grads, now working in finance.
Ryan Palmer shares his chips – sorry – tips for finding the perfect skimming stone
Sam Kay reflects on building a universe
Andrew Stacey explores the mathematics within poetry.
Molly Ireland presents a gambit which will impress your mates
Joe Celko makes a database from card and knitting needles
90 years later, we're still unable to prove this surprisingly simple statement
It doesn’t add up for Patrick Creagh
Aimen Khan ponders how patterns break down
Tyler Helmuth has lost his ant-vocado
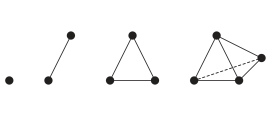
Clem Padin calculates π, but not as we know it
Sophie Bleau explores the differential on Morseback.
Ashleigh Wilcox looks for integer solutions to the Markov equation
Donovan Young goes round the bend exploring what happens when the loop-the-loop goes wrong
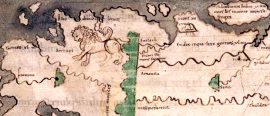
Simone Ramello explores the hic sunt leones of the friendliest numbers we know...
We talk to three teachers, working in different countries
Ricky Li explores the past and future of the soliton
Steven Lockwood finds polygonal numbers hidden in a spreading fire
Henry Jaspars tries to untangle a mixed-up drinks order
Bethany Clarke and Ellen Jolley talk research, raids, and rugby with the Twitch streamer
Today's weather: seasonal, highs of π/18.
Madeleine Hall is a Dedekind-ed follower of fashion
Joe Celko looks at four different abacuses used throughout history
Leszek Wierzchleyski investigates how mathematicians can help surgeons
Paddy MacMahon calculates tangents and turning points without calculus
Thomas Sperling discusses some furry Fermi problems
We talk to three engineers working in different jobs across industry and academia
Alvin Choy works out who will be the last one left in
Madi Hammond shows us how physicists are predicting the fundamental particles of the universe.
James Christian and George Jensen zoom in, out, in, out, and tell us what it's really all about
Graeme Foster asks if there are more odd or even numbers in the triangle
We find out more about the charity's work to support maths education in prisons.
Sophie Bleau chops up, unravels, and squeezes the torus into shape
Sam Harris looks at how Pingu and his friends can stay cosy
Max Hughes investigates how channelling your inner Pythagorean may help you to become the next big lifestyle influencer
Henry Jaspars really likes Nick and Norah’s infinite playlist.
We talk to four statisticians working in different jobs across industry and academia
Eleanor Doman and Qi Zhou swap percentages for placenta-ges
(after Sonnet 130)
Peach Semolina admits her true feelings about science fiction, and delves into the maths of quantum teleportation.
Colin Beveridge barges in and admires some curious railway bridges
Peter Rowlett is gonna need a bigger board
Albert Wood returns to introduce the work that has won mathematics’ most famous award this year.
Michael Wendl really wants those spammers to stop calling him
Nik Alexandrakis explains what they are and what they can tell us
Katie Steckles doesn't understand why any mathematical phenomenon would ever have a not-silly name
We talk to four mathematicians at different stages of their careers
Donovan Young looks at the shapes made when two cones collide
E Adrian Henle, Nick Gantzler, François-Xavier Coudert & Cory Simon team up for a deadly challenge
Goran Newsum always should be someone you really love
Poppy Azmi explores the patterns that are all around us
Mats Vermeeren sketches a simple proof of Noether's first theorem
Chris Boucher explores the secrets and symmetries behind a measure of the distance between binary strings
Callum Ilkiw takes us through a Dungeons and Dragons dice dilemma
Julia Schanen hates being mistaken for a genius.
Sophie Bleau uncovers the secrets behind covering maps
Lucy Rycroft-Smith and Darren Macey unpick the legacy of some of the most ubiquitous names in statistics
Roll up, roll up! Squid Game, hidden harmonies and DnD coming your way in Issue 15. (Plus all the usual nonsense.)
Donovan Young interferes in wave patterns
Madeleine Hall takes a brief dive into the world’s favourite set-relationship-representation diagram.
Forgotten how to draw a log graph? No need to panic – here's a handy guide!
Michael Wendl dissects some variants of the magic separation, a self-working card trick.
Paddy provides a much anticipated update to the most important use of statistical analysis in the last two years
Dimitrios Roxanas tells us why playing chess backwards is the new black (and white).
Tanmay Kulkarni intentionally gets lost on the Tokyo subway
Kimi Chen deciphers the 1920s story you haven’t heard
Hollis Williams explores the power even simple models can have in describing the world around us.
Enter stage left: Chalkdust issue 14. Preorder now!
Sophie Maclean and David Sheard speak to a very top(olog)ical mathematician!
Madeleine Hall explores the sometimes counterintuitive consequences of conditional probability to our everyday lives.
Sophie explores the fascinating mathematics behind the games Mafia and Among Us.
Paddy Moore levels the score
Francisco Berkemeier takes a look at the mathematics behind elections, and the Electoral College, in the United States of America.
The story of an unforgettable mathematician.
Johannes Huber explores the maths behind how image compression works.
Aryan Ghobadi gives a maths lecture at a zoo
A great start to the month of Maying
Maynard manages to prove that 2≠1 in less space than it took Bertrand Russell to prove that 1+1=2
Who is behind the so-called Nobel prize of mathematics? Gerda Grase investigates.
Sam Hartburn attempts the impossible
Emilio McAllister Fognini explores the maths that made Turing so famous
I love Markov is I love Markov chains love me.
Scroggs debates whether sharing truly is caring
Colin counts Countdown's contingent of conundrum causing calculations
James M Christian reflects on chaos
We chat with Trachette about her work in mathematical oncology, her role models, and boosting diversity in mathematics
Kevin Houston teaches us how to deal ourselves the best hand
Mara Kortenkamp, Erin Henning and Anna Maria Hartkopf give us a tour of Polytopia, a home for peculiar polytopes
I like my towns like I like my Alex: Bolton
Sam Hartburn orders wine by the barrel, but wonders if she's getting the most wine
Nobody could draw a space filling curve by hand, but that doesn’t stop Andrew Stacey
Like Fibonacci, but weird. Robert J Low and Thierry Platini explain
Yuliya Nesterova orders some polynomials around
And will we soon all be out of a job? Kevin Buzzard worries us all.
We chat to the crypto chief about inventing RSA... but not being able to tell anyone
Yiannis Petridis connects square roots and continued fractions
Pamela E Harris's story, as told by Talithia Williams
Carmen Cabrera Arnau explores the use of AI in composition
Angela Brett might not be standing on their shoulders
Ever thought about making your own fractal?
Paula Rowińska uses mathematics to answer some awkward questions
Andrei Chekmasov explores order and infinity
Stephen Muirhead meets neither, as he explores waves, tiles and percolation theory
Yuliya Nesterova misses all the pockets, but does manage to solve some cubics
Axel Kerbec gets locked out while exchanging keys
Interviewing Matt was a mistake
Lucy Rycroft-Smith reflects on the use of this well-established measurement
An adventure that starts with a morning of bell ringing and ends with a mad dash in a taxi
Zoe Griffiths investigates paranormal quadratics
Peter Rowlett uses combinatorics to generate caterpillars
How big are these random shapes? Submit an answer for a chance to win a prize!
We chat to the author of the best-selling book How to Bake Pi and pioneer of maths on YouTube
Colin Beveridge looks at different designs for 2- and 3-dimensional tiles
Alex Bolton plays noughts and crosses on unusual surfaces
Read about Maxamillion Polignac's adventures in a prime-hating world
Adam Atkinson uses maths to try to help a sculptor
Elizabeth A Williams falls off a log
Emma Bell explains why the Renaissance mathematician Gerolamo Cardano styled himself as the "man of discoveries".
Just what is category theory? Tai-Danae Bradley explains
Biography of Katherine Johnson, NASA human computer and research mathematician
A tabletop demonstration of chaos.
No more Katie Steckles.
Rob Eastaway joins the dots.
Sam Hartburn bakes your favourite fractal
Zoe Griffiths on the life of e
High stakes gambling with Paula Rowińska
Alex Xela shows us the world of palindromic numbers, and calculates the chances of getting one
Biography of Sir Christopher Zeeman
Infinitely many primes ending in 1, 3, 7 and 9 proved in typically Eulerian style.
Start your quest to conquer the planet with this introduction to the wonderful world of machine learning
Undoubtedly the most influential voice on this hottest of hot topics.
John Dore and Chris Woodcock join the dots
We chat to one of the UK's most qualified voices in mathematics communication
We feel underdressed for Breakfast at Villani's
Staring at your coffee, you wonder whether the light reflecting in cup really is a cardioid curve...
Robert J Low flips one upside down.
We take a proper look at her mathematical accomplishments
A biography of Sophie Bryant
Murder, maths, malaria and mammals
Contemplate the beauty of the Julia and Mandelbrot sets and an elegant mathematical explanation of them
20 questions, the axiom of choice and colouring sequences.
Rediscover linear algebra by playing with circuit diagrams
Explain the strange dynamics of certain insects using game theory
Fermat's Last Theorem with complex powers, wrapped in a story every mathematician can relate to
When slide rules used to rule... find out why they still do
Factorisation is often used in cryptography. But there's something even simpler which turns out to be just as hard.
Folding origami, building networks, making projections and multiple dimensions!
Mary Somerville fights against social mores to become one of the leading mathematicians of her time.
Never be stumped by a maths problem again, with this crash course from the ever-competent Stephen Muirhead
Colin Wright juggles Euler, doodling and Millennium problems
Make your own treasures, guaranteed to be priceless on a future episode of Antiques Roadshow
Pythagoras gave us so much more than a² + b² = c²
Sit in your favourite chair and do away with those tedious algebraic proofs
Diego Carranza tells you to stop worrying and dimensionally analyse the bomb
Solving differential equations instantaneously, using some electrical components and an oscilloscope
More than spirals and rabbits, Fibonacci gave us something much more fundamental.
Counting the divisors of an integer turns out to be a rather hard problem
Why voting systems can never be fair
Teaching a bunch of matchboxes how to play tic-tac-toe
How can we differentiate a function 9¾ times?
Robert Smith? tells us how his favourite matrix saves lives
Why does warm water freeze faster than cold water?
What happens if you play the prisoners' dilemma against yourself?
David Colquhoun explains why more discoveries are false than you thought
The story of how we got the equals sign
Hugh Duncan explores the hidden patterns of fractions
Matthew Scroggs spends too much time beating this arcade classic.
How derivatives of matrices are being used in your day-to-day lives
Here is a very exciting way to measure how similar is your music playlist between your friends, or how similar are your Facebook contacts.
Matthew Wright looks at wormholes in sci-fi
