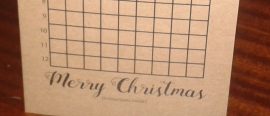24 December 2016
24 December 2016It's the last day of the Chalkdust advent calendar, so there must be something very good behind today's door...
 23 December 2016
23 December 2016Behind today's door... a puzzle!
 22 December 2016
22 December 2016Behind today's door... A book review!
 21 December 2016
21 December 2016Behind today's door... More fascinating facts!
 20 December 2016
20 December 2016Behind today's door... Another carol!
 19 December 2016
19 December 2016Find your perfect partner with this wonderful tree diagram!
 18 December 2016
18 December 2016Behind today's door... A joke!
 17 December 2016
17 December 2016Agony uncle Professor Dirichlet answers your personal problems this Christmastime.
 16 December 2016
16 December 2016Behind today's door... A quiz!
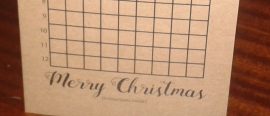 15 December 2016
15 December 2016This year's Chalkdust puzzle Christmas card
 14 December 2016
14 December 2016Santa's sack of scientific surprises
 13 December 2016
13 December 2016Behind today's door... a quiz!
 12 December 2016
12 December 2016Behind today's door... a puzzle!
 11 December 2016
11 December 2016This post was part of the Chalkdust 2016 Advent Calendar. Newton: "Are you going to the Fibonacci themed Christmas party?" Euler: "Yes! I heard it's going to be as big as the two previous years put together."
 10 December 2016
10 December 2016Behind today's door... a good joke!
 9 December 2016
9 December 2016Behind today's door... A binary magic card trick!
 8 December 2016
8 December 2016Winter is coming!
 7 December 2016
7 December 2016Behind today's door... The Chalkdust guide to Christmas presents
 6 December 2016
6 December 2016Behind today's door... a puzzle!
 5 December 2016
5 December 2016And on the fifth day, some rather Algebraic Golden Rings:
 4 December 2016
4 December 2016Behind today's door... a mathematical Christmas Carol
 3 December 2016
3 December 2016Santa's sack of scientific surprises
 2 December 2016
2 December 2016Behind the second door of the advent calendar, there is a puzzle
 1 December 2016
1 December 2016Get into the ChristMATHS spirit with the maths behind the popular Christmas carol!