Issue 15

Covering infinity

Sophie Bleau uncovers the secrets behind covering maps

post

25 May 2022

I’m sure some of you reading this may know about topology vaguely as “that one where the doughnut is the same as the mug”. And you would be right. In essence, topology is maths after you have forgotten what distance is, meaning that space is squishier than we’re used to. Then, the only defining feature of a mug is the hole between its body and its handle and the only defining feature of a doughnut is… well, its hole. A lot of topology is about saying whether one shape is the same as another (such as doughnuts and mugs).

Today we’re going to be going a step further; to ask when two shapes look the same ‘up close’, despite not necessarily being the same overall. For example, if we zoom in closely on any part of a circle, it will look like a line. However these shapes are not the same, since a circle is not a line. We’ll discuss this in more detail soon.

The question I want to answer is whether there is a way to intuitively create a shape that ‘covers’ another. I put it to you that there is. If shape $A$ covers a base shape $B$, there must be a way to map $A$ to $B$ such that

  • the base $B$ is entirely covered by $A$ (ie this is a surjective map); and
  • by zooming on any small patch of $B$, the map looks like the identity map.

The infinite plane covers the torus: the colouring has been added to illustrate how the covering map works.

For instance, we can say that a plane covers a torus. To visualise this, imagine taking the plane, rolling it up into a cylinder, then rolling down the edges of the cylinder, sort of like rolling down a sock. As the edges loop round, the resulting surface is—lo and behold—a torus! This way, every part of the torus is covered (satisfying surjectivity), and every small part of the plane looks like the surface of a torus if you zoom in close enough.

Another example of this is the circle. Any circle can cover another circle by winding round it some number of times. You can imagine that this is like wrapping an elastic band around your finger. Above on the right we have a circle mapping continuously onto a circle a third of its length.

But we can think bigger; the real number line can cover a circle by twisting it round into a helix. This satisfies surjectivity since every part of the circle is covered, and, as mentioned above, every part of the helix looks like a circle if you zoom in close enough. However, a finite interval cannot cover a circle since if we zoom in on the interval’s endpoints, we can’t find any point on the circle that looks like this.

Don’t worry though, our bounded interval can still play with other bounded intervals.

Infinity undercover

So, we’ve seen how to cover lines and circles, but how does this covering business work when lines intersect? The infinity symbol, $\infty$—since I always like to be able to call a symbol something in my head, we’ll pronounce this ‘infty’—has two edges intersecting at one vertex.

This is an example of a graph: a shape consisting of vertices and edges. Each vertex in a graph has a valency, ie the number of ‘arms’ it has. So if two edges meet at a vertex, they become four ‘arms’, and the intersection is a point with valency 4.

Now we can reinterpret the way we think about covers; a circle cannot cover infty since zooming in on the infty at the intersection we have a point where four lines join together, whereas no point on the circle has this property. One idea is to cover this with another infty, using the identity map. But, to make other covers, let’s look at more graphs that are 4-valent at each vertex.

To make sure that we are not mixing up the two arms of each edge, let’s give each edge a direction so we can easily differentiate the ‘source’ end of the edge and the ‘target’… end. Also colouring the edges is a simple way of making sure that we distinguish the two different edges.A constraint for a graph to cover infty is that every vertex in the cover must have two red arrows (one source, one target) and two blue arrows (likewise). Let’s call the graph with arrows a directed graph, or a digraph for short. An example of such a cover is this:

             

                                                                                                                                                  

 

 

 

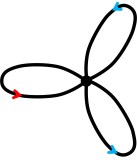From this we get infty by double-looping the blue-edged loop so that the two vertices end up on top of each other, with red edge on red edge and blue edge on blue.

An example of a case where this does not hold is on the right. This does not work for a few reasons. You might have noticed that its vertex has too many arms, or that there is more than one blue arrow pointing towards/away from the vertex. Is there some other way to colour and direct the graph to make it a cover of infty? Well, whichever colouring we choose, we will always have more than two of one colour. So sadly, I topologise: this graph is not destined to cover infinity.

Inftys all the way down

Another cover is the infinite grid. A way to conceptualise this map is thinking similarly to the example of the plane rolling up to make the torus. First we roll the graph into a vertical cylinder, then we roll the edges of this cylinder down so that each rung is mapped onto the same one.  Up until this point, taking a red path then a blue path in each cover will end up at the same point as taking a blue path and then red (try this out on the infinite grid). But can we break this pattern?

Here we find a special case I call the fractal cross, where the cover is so intricate that the path between any two vertices is unique. Try starting at any vertex on the graph, and mark out the path travelling red then blue. Now go back and do the same with blue then red. Your destination depends on the order of your steps! I call this the fractal cross because it is infinitely detailed—like a fractal. The fractal cross covers infty in a similar way to the infinite grid. This, *drum roll please*, is the largest cover of infty. More precisely, it covers every other cover of infty and nothing else covers it.

From cross to cover

All covers of infty can actually be derived from the fractal cross. As an example, if we take the central blue line of the graph, we can first wrap it around itself in the way that a line covers a circle; and then glue together all the branching red arms, and we will get this cover:

By repeatedly gluing and warping the fractal cross we can find more covers, and eventually get down to infty.

For instance, let’s again take a blue-edged line on the fractal cross, but this time wind it around until every third blue edge in the line is glued together creating a loop. Now do the same with a red-edged line intersecting this loop. Next glue the vertices of the loops together one by one. As you can see, this forms a triangle with vertices intersecting a circle. Finally this graph with six edges collapses down onto infty.

Illuminati confirmed?

Every cover we’ve looked at so far has been 4-valent; in fact we have now recognised the 4-valency of every vertex in the cover as a necessary condition to be a cover. But is it a sufficient condition? If we have a 4-valent graph, will it necessarily cover infinity?

We can generate complex, and often infinite covers of infty, all just by checking all our rules are satisfied. In this way, we have a surprising amount of flexibility to build up such a cover. You might enquire further; how much flexibility? Can we explore some artistic licence?

For example, would a Celtic knot cover infty? A Celtic knot is a traditional weaving pattern, which is drawn like a rope tied in a knot, with the notable property that the two rope ends are stuck together. If we shine a torch on such a knot and take a picture of its shadow, we can imagine that the resulting silhouette is a graph. All vertices of this shadow graph will be 4-valent since it is the junction of two lines crossing. So… does this cover infty?

A beautiful Celtic knot designed by Leonardo da Vinci is shown on the right. Below, I have drawn the digraph associated with the centre piece, verifying both that it indeed covers infty, and that I have far too much time on my hands. In fact, we find that a Celtic knot’s shadow will always qualify as a cover of infty. This is to say that there will always be a digraph of the knot satisfying the requirements—each vertex having a blue source, blue target, red source, and red target.

For the interested reader, the fact that the shadow of any knot diagram can be made to cover infty follows from a few neat ideas in knot theory. First, the shadow of a knot diagram is, by definition a planar graph, and it is possible to ‘chessboard colour’ the complementary regions of this graph, ie colour those regions black or white so that no adjacent regions have the same colour. (There are several ways to prove this, one way being to prove that the graph ‘dual’ to the complementary regions contains no odd-length cycles by the definition of a knot.) Now choose an orientation of the knot, which gives an orientation of each edge in the shadow graph. Assign an edge the colour red if the region on its right is black, and blue otherwise. In this way the graph can be directed and coloured, and it is straightforward to check that every vertex has four arms, two red and two blue, and one incoming and one outgoing of each colour. This means the graph covers infty. In fact one can even prove that every regular 4-valent graph covers infty, but this is trickier, using the so-called 2-factor theorem.

It is fascinating that an artistic piece could relate to such a mathematical idea as a topological cover, and all of this stemming from the theory of a torus being considered topologically identical to a mug—who would have thought? The realisation that all knots (apart from the circle) cover infty is non-trivial and—in my opinion—really cool. However, as cool as topological space is, just make sure you don’t try pouring any tea in your doughnut!

Sophie is a PhD student at the University of Edinburgh. She spends her free time drawing Celtic knots and fangirling over Leonardo da Vinci. She has a cat called Norma, who takes great pleasure disrupting any mathematical progress—usually by sitting on it.
All articles by Sophie

More from Chalkdust