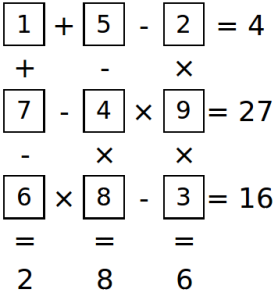Answers to “Can you solve these puzzles?”

Make the Sums

Unit Octagon

Name the regions as follows:

$E$ is a 1×1 square. Placed together, $A$, $C$, $G$ and $I$ also make a 1×1 square. $B$ is equal to $H$ and $D$ is equal to $F$.
Therefore $B+E+F=A+C+D+G+H+I$. Therefore the hatched region is $C$ larger than the shaded region. The area of $C$ (and therefore the difference) is $\frac{1}{4}$.

Reverse Bases

If $ab$ in base 10 is equal to $ba$ in base 4, then $10a+b=4b+a$. So, $9a=3b$. $a$ and $b$ must both be less than 4, as they are digits used in base 4, so $a=1$ and $b=3$. So 13 in base 10 is equal to 31 in base 4.

By the same method, we find that:

• 23 in base 10 is equal to 32 in base 7.
• 46 in base 10 is equal to 64 in base 7.
• 12 in base 9 is equal to 21 in base 5.
• 24 in base 9 is equal to 42 in base 5.