6 December 2023Can you solve it?
1 May 2021Looking for a challenge? Try our cryptic crossnumber—with hints and tips so anyone can have a go!
25 December 2020Puzzle #2 in our 2020 Christmas puzzle series
24 December 2020Puzzle #1 in our 2020 Christmas puzzle series
17 April 2020Adam Townsend sets the fifth and final puzzle. Can you solve it?
- 17 April 2020
Humbug sets the fourth puzzle. Can you solve it?
- 17 April 2020
David Sheard sets the third puzzle. Can you solve it?
- 17 April 2020
TD Dang sets the second puzzle. Can you solve it?
- 17 April 2020
Celebrate the launch of issue 11 by taking part in our puzzle hunt
- 17 April 2020
Matthew Scroggs sets the first puzzle. Can you solve it?
18 October 2018Win £100 of Maths Gear goodies by solving our famously fiendish crossnumber
- 12 March 2018
Win £100 of Maths Gear goodies by solving our famously fiendish crossnumber
18 January 2018A fiendish puzzle for you to 'pour' over...
22 December 2017Can you solve four puzzles to reveal the hidden message?
18 December 2017Try our nonograms! And remember, not all puzzles have a unique solution...
11 December 2017Solve this and you could be the lucky winner of a signed copy of The Indisputable Existence of Santa Claus
4 December 2017Solve this and you could be the lucky winner of a Chalkdust T-shirt
18 October 2017Win £100 of Maths Gear goodies by solving our famously fiendish crossnumber
29 June 2017Have a go at these puzzles, adequate for your holidays!
- 6 March 2017
Win £100 of Maths Gear goodies by solving our famously fiendish crossnumber
6 March 2017Solve the puzzles that appeared in Issue 05.
23 December 2016Behind today's door... a puzzle!
12 December 2016Behind today's door... a puzzle!
- 6 December 2016
Behind today's door... a puzzle!
- 2 December 2016
Behind the second door of the advent calendar, there is a puzzle
3 October 2016Never be stumped by a maths problem again, with this crash course from the ever-competent Stephen Muirhead
- 3 October 2016
Solve the puzzles that appeared in Issue 04.
- 3 October 2016
Can you solve it?
14 July 2016Can you solve these puzzles about differentiation and integration?
- 19 June 2016
All the fun of our prize crossnumber, just smaller and without a prize
14 April 2016This month's round up of mathematical blog posts.
17 March 2016How many points could you have scored at our launch quiz?
- 13 March 2016
Solve the puzzles that appeared in Issue 03.
- 24 December 2015
Something for you to solve during the post-Christmas lull
- 6 October 2015
These puzzles appeared in Issue 02 of the magazine.
- 3 September 2015
While we work on issue 2
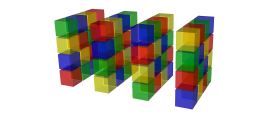20 August 2015Can you solve our 3D Sudoku puzzles?
31 July 2015These puzzles appeared in the Chalkdust newsletters. You can find the answers here and sign up for the newsletter here.
16 July 2015How to make Sudoku more interesting
- 7 July 2015
These puzzles appeared in Issue 01 of the magazine.
11 June 2015If you enjoyed Hannah's sweets then you'll love these...
14 May 2015Pub ✕ maths = ?
24 March 2015Our original £100 prize crossnumber. Download and enjoy!
