Puzzle Solutions, Issue 02

Seven Digits

Let’s call my number $n$. If the number is squared twice then multiplied by $n$, we get $n^5$.

For all integers $n$, the final digit of $n^5$ is the same as the final digit of $n$. In other words:

$$n^5\equiv n \mod 10$$

Therefore, the final digit of Dr. Dingo’s number is 7.

$$7^5=16807$$
$$17^5=1419857$$
$$27^5=14348907$$

So, in order for the answer to have seven digits, Dr. Dingo’s number was 17.

Odd Squares

If $n^2$ has all odd digits then the units digit of $n$ must be odd. It can be checked that $n$ cannot be a one digit number (except 1 or 3 as given in the question) as the tens digit will be even.
Therefore n can be written as $10A+B$ where $A$ is a positive integer and $B$ is an odd positive integer.
$$n^2=(10A+B)^2\\=100A+20AB+B^2$$
Now consider the tens digit of this.
$100A$ has no effect on this digit. The tens digit of $20AB$ will be the units digit of $2AB$ which will be even. The tens digit of $B^2$ is even (as checked above). Therefore the tens digit of $n^2$ is even.
Hence 1 and 9 are the only square numbers where all the digits are odd.

Folding Tube Maps

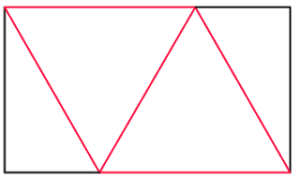
Once the map is folded, it will look like this:

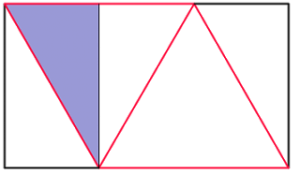
For the final tetrahedron to be regular, the red lengths must be equal. Let each red length be 2 (this will get rid of halves in the upcoming calculations). By drawing a vertical line in we can work out the width and height of the rectangle:

The width of the rectangle is 3 (one and a half red lengths). Using Pythagoras’ Theorem in the blue triangle, we find that the height of the rectangle is $\sqrt{3}$. Therefore, the ratio of the rectangle is $3:\sqrt{3}$ or $1:\sqrt{3}$.