 17 March 2025
17 March 2025Can you solve it?
 17 March 2025
17 March 2025Suits, sofas and sculptures punctuate the prof's postbag this issue
 17 March 2025
17 March 2025We announce the winners of this coveted prize
 17 March 2025
17 March 2025Can you solve it?
 8 November 2024
8 November 2024Can you solve it?
 8 November 2024
8 November 2024Stranded in Scotland's capital? This guide will keep you busy
 8 November 2024
8 November 2024Cricket, coursework and karaoke are among the problems solved in this issue's Dear Dirichlet agony aunt column
 8 November 2024
8 November 2024Can you solve it?
 20 May 2024
20 May 2024Game shows, flight and social media bots are among the problems solved in this issue's Dear Dirichlet agony aunt column
 20 May 2024
20 May 2024Can you solve it?
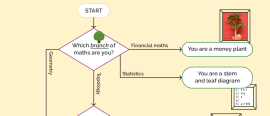 20 May 2024
20 May 2024Find out by following our simple flowchart
 20 May 2024
20 May 2024QED or $\square$?
 6 December 2023
6 December 2023Can you solve it?
 6 December 2023
6 December 2023Today's weather: seasonal, highs of π/18.
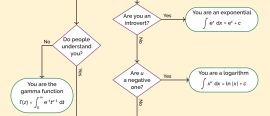 6 December 2023
6 December 2023And more importantly, are you on the A-level formula sheet?
 6 December 2023
6 December 2023Can you solve it?
 22 May 2023
22 May 2023Canines, Cliff Richard and conditioning find their way into the prof's postbox this issue.
 22 May 2023
22 May 2023Can you solve it?
 22 May 2023
22 May 2023Just answer these EIGHT simple questions!
 22 May 2023
22 May 2023The best and worst from this year's Met Gala
 9 November 2022
9 November 2022Find out by answering six simple questions
 9 November 2022
9 November 2022Can you solve it?
 9 November 2022
9 November 2022Follow these simple steps to frustrate anyone who ever dreamed of using their light saber on the USS Enterprise
 9 November 2022
9 November 2022Albert Wood returns to introduce the work that has won mathematics’ most famous award this year.
 25 May 2022
25 May 2022Win a £100 Maths Gear goody bag by solving our infamous puzzle
 25 May 2022
25 May 2022Weddings, holidays and catfish find their way into the prof's postbox this issue.
 25 May 2022
25 May 2022Goran Newsum always should be someone you really love
 25 May 2022
25 May 2022Can you solve it?
 22 November 2021
22 November 2021Win a £100 Maths Gear goody bag by solving our infamous puzzle
 22 November 2021
22 November 2021Football, telly and shape-shifting houses find their way into the prof's postbox this issue.
 22 November 2021
22 November 2021Forgotten how to draw a log graph? No need to panic – here's a handy guide!
 22 November 2021
22 November 2021Can you solve it?
 1 May 2021
1 May 2021Issue 13 is here! Find out how to get involved with our mathematical art launch project
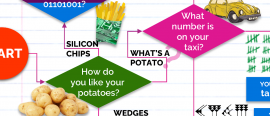 1 May 2021
1 May 2021Are you binary? Roman numerals? The decimals? Find out by answering a maximum of ∞ easy questions
 1 May 2021
1 May 2021£100 of Maths Gear goodies to be won if you can solve it
 1 May 2021
1 May 2021Parishoners, partners and puzzled playwrights have written in to the professor's postbox this issue
 30 October 2020
30 October 2020Books, business and barns are the topics readers have sent in to the professor's postbox this issue
 30 October 2020
30 October 2020£100 of MathsGear goodies to be won if you can solve it
 30 October 2020
30 October 2020A handy tool that can make writing great tweets much easier
 30 October 2020
30 October 2020Sam Hartburn attempts the impossible
 17 April 2020
17 April 2020£100 of MathsGear goodies to be won if you can solve it
 17 April 2020
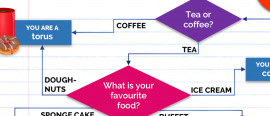
17 April 2020Are you a torus? A cone? Ed Spheran? Find out by answering a maximum of five easy questions
 17 April 2020
17 April 2020Grant applications, musical media and last-minute Olympics training are the topics readers have sent in to the professor's postbox this issue
 17 April 2020
17 April 2020Sam Hartburn orders wine by the barrel, but wonders if she's getting the most wine
 23 October 2019
23 October 2019Can you solve it?
 23 October 2019
23 October 2019Letter writing, hospital visits, and getting the family active are among the topics of discussion in this issue's Dear Dirichlet advice column
 23 October 2019
23 October 2019Part 7 of our mathematical comic's adventure
 23 October 2019
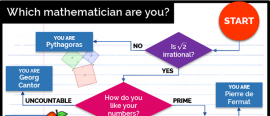
23 October 2019How do you like your numbers? Prime? Positive but infinitely small? Find out which famous mathematician you are
 14 March 2019
14 March 2019Win £100 of Maths Gear goodies by solving our famously fiendish crossnumber
 14 March 2019
14 March 2019Coffee, Brexit and badgers are among the topics of discussion in this issue's Dear Dirichlet advice column
 14 March 2019
14 March 2019Mystic mug has some predictions for you...
 14 March 2019
14 March 2019The definitive chart of the best Chalkdust regulars
 18 October 2018
18 October 2018Print it out and play against your friends!
 18 October 2018
18 October 2018Win £100 of Maths Gear goodies by solving our famously fiendish crossnumber
 18 October 2018
18 October 2018Read about Maxamillion Polignac's adventures in a prime-hating world
 18 October 2018
18 October 2018Village fetes, Brexit and flowers are among the topics of discussion in this issue's Dear Dirichlet advice column
 12 March 2018
12 March 2018Pigs, popes and produce are among the topics of discussion in this issue's Dear Dirichlet advice column
 12 March 2018
12 March 2018Win £100 of Maths Gear goodies by solving our famously fiendish crossnumber
 12 March 2018
12 March 2018Zoe Griffiths on the life of e
 12 March 2018
12 March 2018Part 6 of our mathematical comic's adventure
 18 October 2017
18 October 2017Win £100 of Maths Gear goodies by solving our famously fiendish crossnumber
 18 October 2017
18 October 2017Prof. Dirichlet tackles archaeology and supercomputers in answering your personal problems
 18 October 2017
18 October 2017Part 5 of our mathematical comic's adventure
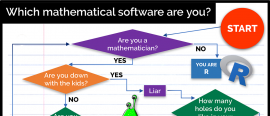 18 October 2017
18 October 2017"R" you a Matlab or a Python? Fortran or Mathematica? Find out which package suits you best.
 6 March 2017
6 March 2017Win £100 of Maths Gear goodies by solving our famously fiendish crossnumber
 6 March 2017
6 March 2017Prof. Dirichlet tackles political arguments and werewolves in answering your personal problems
 6 March 2017
6 March 2017Part 4 of our mathematical comic's adventure
 6 March 2017
6 March 2017Are you feeling ideal? In your prime? Discover your inner mathematical object (plus handy term explainer).
 6 March 2017
6 March 2017The definitive chart of the circle's greatest parts
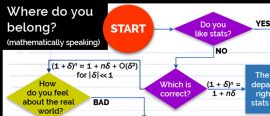 3 October 2016
3 October 2016Follow our flowchart to find out where your true calling is
 3 October 2016
3 October 2016Part 3 of our mathematical comic's adventure
 3 October 2016
3 October 2016Don't be left behind... more mathematical fashion advice
 3 October 2016
3 October 2016Win £100 of maths goodies in our fiendish crossnumber
 13 March 2016
13 March 2016Find out what the future holds for you... or maybe just a box of scorpions.
 13 March 2016
13 March 2016Part 2 of our mathematical comic's adventure
 13 March 2016
13 March 2016Are you a FX-82 or an FX-85 fan?
 6 October 2015
6 October 2015Platonic shapes from tube maps, flexagons, and more mathematical craft
 6 October 2015
6 October 2015Continue the journey of the Inverse Homotopy...
 16 April 2015
16 April 2015Moonlighting agony uncle Professor Dirichlet answers your personal problems















































































