22 May 2023We find out more about the charity's work to support maths education in prisons.
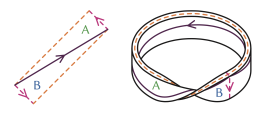
22 May 2023Sophie Bleau chops up, unravels, and squeezes the torus into shape
22 May 2023Sam Harris looks at how Pingu and his friends can stay cosy
22 May 2023Max Hughes investigates how channelling your inner Pythagorean may help you to become the next big lifestyle influencer
22 May 2023Henry Jaspars really likes Nick and Norah’s infinite playlist.
22 May 2023We talk to four statisticians working in different jobs across industry and academia
22 May 2023Eleanor Doman and Qi Zhou swap percentages for placenta-ges
22 May 2023(after Sonnet 130)
9 November 2022Peach Semolina admits her true feelings about science fiction, and delves into the maths of quantum teleportation.
9 November 2022Colin Beveridge barges in and admires some curious railway bridges
9 November 2022Peter Rowlett is gonna need a bigger board
9 November 2022Albert Wood returns to introduce the work that has won mathematics’ most famous award this year.
9 November 2022Michael Wendl really wants those spammers to stop calling him
9 November 2022Nik Alexandrakis explains what they are and what they can tell us
9 November 2022Katie Steckles doesn't understand why any mathematical phenomenon would ever have a not-silly name
9 November 2022We talk to four mathematicians at different stages of their careers
9 November 2022Donovan Young looks at the shapes made when two cones collide
25 May 2022E Adrian Henle, Nick Gantzler, François-Xavier Coudert & Cory Simon team up for a deadly challenge
25 May 2022Goran Newsum always should be someone you really love
25 May 2022Poppy Azmi explores the patterns that are all around us
25 May 2022Mats Vermeeren sketches a simple proof of Noether's first theorem
25 May 2022Chris Boucher explores the secrets and symmetries behind a measure of the distance between binary strings
25 May 2022Callum Ilkiw takes us through a Dungeons and Dragons dice dilemma
25 May 2022Julia Schanen hates being mistaken for a genius.
25 May 2022Sophie Bleau uncovers the secrets behind covering maps
25 May 2022Lucy Rycroft-Smith and Darren Macey unpick the legacy of some of the most ubiquitous names in statistics
16 May 2022Roll up, roll up! Squid Game, hidden harmonies and DnD coming your way in Issue 15. (Plus all the usual nonsense.)
22 November 2021Donovan Young interferes in wave patterns
22 November 2021Madeleine Hall takes a brief dive into the world’s favourite set-relationship-representation diagram.
22 November 2021Forgotten how to draw a log graph? No need to panic – here's a handy guide!
22 November 2021Michael Wendl dissects some variants of the magic separation, a self-working card trick.
22 November 2021Paddy provides a much anticipated update to the most important use of statistical analysis in the last two years
22 November 2021Dimitrios Roxanas tells us why playing chess backwards is the new black (and white).
22 November 2021Tanmay Kulkarni intentionally gets lost on the Tokyo subway
22 November 2021Kimi Chen deciphers the 1920s story you haven’t heard
22 November 2021Hollis Williams explores the power even simple models can have in describing the world around us.
15 November 2021Enter stage left: Chalkdust issue 14. Preorder now!
1 May 2021Sophie Maclean and David Sheard speak to a very top(olog)ical mathematician!
1 May 2021Madeleine Hall explores the sometimes counterintuitive consequences of conditional probability to our everyday lives.
1 May 2021Sophie explores the fascinating mathematics behind the games Mafia and Among Us.
- 1 May 2021
Paddy Moore levels the score
1 May 2021Francisco Berkemeier takes a look at the mathematics behind elections, and the Electoral College, in the United States of America.
1 May 2021The story of an unforgettable mathematician.
1 May 2021Johannes Huber explores the maths behind how image compression works.
1 May 2021Aryan Ghobadi gives a maths lecture at a zoo
27 April 2021A great start to the month of Maying
30 October 2020Maynard manages to prove that 2≠1 in less space than it took Bertrand Russell to prove that 1+1=2
30 October 2020Who is behind the so-called Nobel prize of mathematics? Gerda Grase investigates.
30 October 2020Sam Hartburn attempts the impossible
30 October 2020Emilio McAllister Fognini explores the maths that made Turing so famous
30 October 2020I love Markov is I love Markov chains love me.
30 October 2020Scroggs debates whether sharing truly is caring
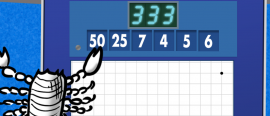30 October 2020Colin counts Countdown's contingent of conundrum causing calculations
30 October 2020James M Christian reflects on chaos
17 April 2020We chat with Trachette about her work in mathematical oncology, her role models, and boosting diversity in mathematics
17 April 2020Kevin Houston teaches us how to deal ourselves the best hand
17 April 2020Mara Kortenkamp, Erin Henning and Anna Maria Hartkopf give us a tour of Polytopia, a home for peculiar polytopes
17 April 2020I like my towns like I like my Alex: Bolton
17 April 2020Sam Hartburn orders wine by the barrel, but wonders if she's getting the most wine
17 April 2020Nobody could draw a space filling curve by hand, but that doesn’t stop Andrew Stacey
17 April 2020Like Fibonacci, but weird. Robert J Low and Thierry Platini explain
17 April 2020Yuliya Nesterova orders some polynomials around
23 October 2019And will we soon all be out of a job? Kevin Buzzard worries us all.
23 October 2019We chat to the crypto chief about inventing RSA... but not being able to tell anyone
23 October 2019Yiannis Petridis connects square roots and continued fractions
23 October 2019Pamela E Harris's story, as told by Talithia Williams
23 October 2019Carmen Cabrera Arnau explores the use of AI in composition
23 October 2019Angela Brett might not be standing on their shoulders
23 October 2019Ever thought about making your own fractal?
23 October 2019Paula Rowińska uses mathematics to answer some awkward questions
23 October 2019Andrei Chekmasov explores order and infinity
14 March 2019Stephen Muirhead meets neither, as he explores waves, tiles and percolation theory
14 March 2019Yuliya Nesterova misses all the pockets, but does manage to solve some cubics
14 March 2019Axel Kerbec gets locked out while exchanging keys
14 March 2019Interviewing Matt was a mistake
14 March 2019Lucy Rycroft-Smith reflects on the use of this well-established measurement
14 March 2019An adventure that starts with a morning of bell ringing and ends with a mad dash in a taxi
14 March 2019Zoe Griffiths investigates paranormal quadratics
14 March 2019Peter Rowlett uses combinatorics to generate caterpillars
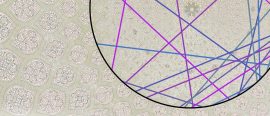14 March 2019How big are these random shapes? Submit an answer for a chance to win a prize!
18 October 2018We chat to the author of the best-selling book How to Bake Pi and pioneer of maths on YouTube
18 October 2018Colin Beveridge looks at different designs for 2- and 3-dimensional tiles
18 October 2018Alex Bolton plays noughts and crosses on unusual surfaces
18 October 2018Read about Maxamillion Polignac's adventures in a prime-hating world
18 October 2018Adam Atkinson uses maths to try to help a sculptor
18 October 2018Elizabeth A Williams falls off a log
18 October 2018Emma Bell explains why the Renaissance mathematician Gerolamo Cardano styled himself as the "man of discoveries".
18 October 2018Just what is category theory? Tai-Danae Bradley explains
18 October 2018Biography of Katherine Johnson, NASA human computer and research mathematician
18 October 2018A tabletop demonstration of chaos.
12 March 2018No more Katie Steckles.
12 March 2018Rob Eastaway joins the dots.
12 March 2018Sam Hartburn bakes your favourite fractal
12 March 2018Zoe Griffiths on the life of e
12 March 2018High stakes gambling with Paula Rowińska
12 March 2018Alex Xela shows us the world of palindromic numbers, and calculates the chances of getting one
12 March 2018Biography of Sir Christopher Zeeman
12 March 2018Infinitely many primes ending in 1, 3, 7 and 9 proved in typically Eulerian style.
12 March 2018Start your quest to conquer the planet with this introduction to the wonderful world of machine learning
12 March 2018Undoubtedly the most influential voice on this hottest of hot topics.
12 March 2018John Dore and Chris Woodcock join the dots
12 March 2018We chat to one of the UK's most qualified voices in mathematics communication
18 October 2017We feel underdressed for Breakfast at Villani's
18 October 2017Staring at your coffee, you wonder whether the light reflecting in cup really is a cardioid curve...
18 October 2017Robert J Low flips one upside down.
18 October 2017We take a proper look at her mathematical accomplishments
18 October 2017A biography of Sophie Bryant
18 October 2017Murder, maths, malaria and mammals
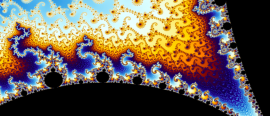
18 October 2017Contemplate the beauty of the Julia and Mandelbrot sets and an elegant mathematical explanation of them
18 October 201720 questions, the axiom of choice and colouring sequences.
6 March 2017Rediscover linear algebra by playing with circuit diagrams
6 March 2017Explain the strange dynamics of certain insects using game theory
6 March 2017Fermat's Last Theorem with complex powers, wrapped in a story every mathematician can relate to
6 March 2017When slide rules used to rule... find out why they still do
6 March 2017Factorisation is often used in cryptography. But there's something even simpler which turns out to be just as hard.
6 March 2017Folding origami, building networks, making projections and multiple dimensions!
- 6 March 2017
Mary Somerville fights against social mores to become one of the leading mathematicians of her time.
3 October 2016Never be stumped by a maths problem again, with this crash course from the ever-competent Stephen Muirhead
3 October 2016Colin Wright juggles Euler, doodling and Millennium problems
3 October 2016Make your own treasures, guaranteed to be priceless on a future episode of Antiques Roadshow
3 October 2016Pythagoras gave us so much more than a² + b² = c²
3 October 2016Sit in your favourite chair and do away with those tedious algebraic proofs
3 October 2016Diego Carranza tells you to stop worrying and dimensionally analyse the bomb
13 March 2016Solving differential equations instantaneously, using some electrical components and an oscilloscope
- 13 March 2016
More than spirals and rabbits, Fibonacci gave us something much more fundamental.
13 March 2016Counting the divisors of an integer turns out to be a rather hard problem
13 March 2016Why voting systems can never be fair
13 March 2016Teaching a bunch of matchboxes how to play tic-tac-toe
13 March 2016How can we differentiate a function 9¾ times?
6 October 2015Robert Smith? tells us how his favourite matrix saves lives
6 October 2015Why does warm water freeze faster than cold water?
6 October 2015What happens if you play the prisoners' dilemma against yourself?
6 October 2015David Colquhoun explains why more discoveries are false than you thought
- 6 October 2015
The story of how we got the equals sign
6 October 2015Hugh Duncan explores the hidden patterns of fractions
24 March 2015Matthew Scroggs spends too much time beating this arcade classic.
24 March 2015How derivatives of matrices are being used in your day-to-day lives
24 March 2015Here is a very exciting way to measure how similar is your music playlist between your friends, or how similar are your Facebook contacts.
24 March 2015Matthew Wright looks at wormholes in sci-fi
