18 June 2025
18 June 2025Calling all final-year students! This is your opportunity to get your work published as a Chalkdust article.
 17 March 2025
17 March 2025Molly Ireland shares her experience of winning our first ever dissertation prize!
 12 March 2025
12 March 2025Pre-order your copy of issue 21 now!
 1 November 2024
1 November 2024Pre-order your copy of our 9½-year anniversary issue now!
 27 May 2024
27 May 2024Calling all final-year students!
 9 May 2024
9 May 2024Pre-order your copy now!
 21 March 2024
21 March 2024We review the seventh of this year's nominees for Book of the Year
 19 March 2024
19 March 2024We review the sixth of this year's nominees for Book of the Year
 14 March 2024
14 March 2024We review the fifth of this year's nominees for Book of the Year
 12 March 2024
12 March 2024We review the fourth of this year's nominees for Book of the Year
 11 March 2024
11 March 2024We review the third of this year's nominees for Book of the Year
 5 March 2024
5 March 2024We review the second of this year's nominees for Book of the Year
 29 February 2024
29 February 2024We review the first of this year's nominees for Book of the Year
 27 February 2024
27 February 2024We announce the shortlist of our favourite maths-themed books of last year
 14 May 2023
14 May 2023Pre-order a copy and/or book your ticket for our launch event
 1 December 2022
1 December 2022A tribute to alumni Roly Drower by Hugh Duncan
 8 November 2022
8 November 2022Did you solve it?
 7 November 2022
7 November 2022Hear ye! Hear ye! Chalkdust Magazine issue 16 is launching, full of mathematical joy and curiosity.
 16 May 2022
16 May 2022Roll up, roll up! Squid Game, hidden harmonies and DnD coming your way in Issue 15. (Plus all the usual nonsense.)
 31 March 2022
31 March 2022We announce the shortlist of our favourite maths-themed books of last year
 15 November 2021
15 November 2021Enter stage left: Chalkdust issue 14. Preorder now!
 4 November 2021
4 November 2021Did you solve it?
 1 May 2021
1 May 2021Did you solve it?
 1 May 2021
1 May 2021Issue 13 is here! Find out how to get involved with our mathematical art launch project
 27 April 2021
27 April 2021A great start to the month of Maying
 15 March 2021
15 March 2021We announce the winner of this coveted prize
 9 March 2021
9 March 2021We review the seventh of this year's nominees for the Book of the Year, and open the vote for the readers' favourite
 9 March 2021
9 March 2021We review the sixth of this year's nominees for the Book of the Year
 4 March 2021
4 March 2021We review the fifth of this year's nominees for the Book of the Year
 2 March 2021
2 March 2021We review the fourth of this year's nominees for the Book of the Year
 1 March 2021
1 March 2021We review the third of this year's nominees for the Book of the Year
 23 February 2021
23 February 2021We review the second of this year's nominees for the Book of the Year
 22 February 2021
22 February 2021We review the first of this year's nominees for the Book of the Year
 15 February 2021
15 February 2021We announce the shortlist
 14 January 2021
14 January 2021Łukasz takes us on a tour through a surprisingly diverse range of algorithms to test for divisibility by 7
 2 January 2021
2 January 2021We reveal the solutions to our Christmas puzzles!
 26 December 2020
26 December 2020Puzzle #3 in our 2020 Christmas puzzle series
 25 December 2020
25 December 2020Puzzle #2 in our 2020 Christmas puzzle series
 24 December 2020
24 December 2020Puzzle #1 in our 2020 Christmas puzzle series
 11 December 2020
11 December 2020Belgin gets hooked on a classic maths game...in 16 bits! Here's her review...
 26 November 2020
26 November 2020Try out these flo-maps for yourself: fractions speak louder than words
 26 November 2020
26 November 2020Hugh Duncan returns with the long-awaited prequel in which he further explores the geometric patterns hidden behind the fractions.
 10 November 2020
10 November 2020Now available to catch up on YouTube
 1 October 2020
1 October 2020Did you solve it?
 9 April 2020
9 April 2020Issue 11 of everyone's favourite magazine for the mathematically curious is coming very soon
 26 March 2020
26 March 2020Did you solve it?
 5 March 2020
5 March 2020Issah Merchant discusses the geometric principles behind, and real-world applications of, curvature
 27 February 2020
27 February 2020We announce the winner of this coveted prize
 20 February 2020
20 February 2020We review the ninth of this year's nominees for the Book of the Year
 19 February 2020
19 February 2020We review the eighth of this year's nominees for the Book of the Year
 18 February 2020
18 February 2020We review the sevnth of this year's nominees for the Book of the Year
 17 February 2020
17 February 2020We review the sixth of this year's nominees for the Book of the Year
 16 February 2020
16 February 2020We review the fifth of this year's nominees for the Book of the Year
 10 February 2020
10 February 2020We review the fourth of this year's nominees for the Book of the Year
 6 February 2020
6 February 2020We review the third of this year's nominees for the Book of the Year
 4 February 2020
4 February 2020We review the second of this year's nominees for the Book of the Year
 3 February 2020
3 February 2020We review the first of this year's nominees for the Book of the Year
 30 January 2020
30 January 2020We reveal the shortlist
 10 December 2019
10 December 201921 simple steps to draw your own Islamic pattern!
 23 October 2019
23 October 2019This article will (unsurprisingly) tell you how to crochet a fractal
 15 October 2019
15 October 2019Come along to our launch party for free pizza and the real quiz
 1 October 2019
1 October 2019A month celebrating the contributions of black mathematicians
 27 September 2019
27 September 2019Did you solve it?
 1 August 2019
1 August 2019Hugh Duncan explores an exciting variation on Conway's Game of Life
 6 June 2019
6 June 2019We have a go at the puzzles in Daniel Griller’s new book
 23 May 2019
23 May 2019W.L. Feldhusen explains the obscure sine-finding trick hiding inside your calculator!
 2 May 2019
2 May 2019Tony Pisculli dissects the lyrics from a popular song
 18 April 2019
18 April 2019The scientific story behind the cover of Joy Division's treasured debut
 28 March 2019
28 March 2019In 2018, scientists discovered a new shape that is essential to multicellular life
 8 March 2019
8 March 2019Celebrate International Women's day by reading about rebel women in mathematics!
 7 March 2019
7 March 2019More sartorial inquisition for your feet
 1 March 2019
1 March 2019Read the magazine, and come to the launch party!
 28 February 2019
28 February 2019A podcast for the mathematically curious
 21 February 2019
21 February 2019Did the Danish mathematician also sail the high seas?
 14 February 2019
14 February 2019Did you solve it?
 7 February 2019
7 February 2019Tricks and puzzles that provide an introduction to the world of partitions
 31 January 2019
31 January 2019A podcast for the mathematically curious
 24 January 2019
24 January 2019How can we teach people about the sieve in a way that helps them best understand prime numbers?
 17 January 2019
17 January 2019Investigating the power of thinking rationally
 10 January 2019
10 January 2019Looking back at puzzles about complex numbers, tic-tac-toe, and the Eggnog Mystery
 2 January 2019
2 January 2019Lies, liquor and logical deduction play their part in this festive holiday tale
 18 December 2018
18 December 2018Why do Christmas lights get tangled? And what's the perfect way to decorate a Christmas tree? Find the answers here.
 14 December 2018
14 December 2018Win this year's best book of geometry puzzles
 11 December 2018
11 December 2018Looking back at the exciting day that closed our 2018 celebrations
 6 December 2018
6 December 2018Win a DVD boxset from Festival of the spoken nerd in our first Christmas competition!
 29 November 2018
29 November 2018Mike Fletcher explores the optimal strategy for winning the popular television game show
 22 November 2018
22 November 2018Bring your shovel, and dig with us to unearth some amazing results about polynomials
 16 November 2018
16 November 2018A podcast for the mathematically curious
 15 November 2018
15 November 2018Hugh Duncan explores polygons with a shortage of edges
 8 November 2018
8 November 2018What is pi? How do we define it and who first thought of it? We explore the history of this quintessential mathematical constant.
 1 November 2018
1 November 2018Introducing Mathscon, a mathematics conference with a difference!
 30 October 2018
30 October 2018John Pougué Biyong explains how and why science communication can lead to better diversity.
 25 October 2018
25 October 2018Reviewing the Royal Institution's first Black History Month event.
 11 October 2018
11 October 2018Nira Chamberlain explains how Black Panther's suit can be modelled mathematically
 9 October 2018
9 October 2018Clive Fraser reflects on his interactions with one of the greatest ever Black mathematicians
 9 October 2018
9 October 2018This month’s round up of mathematical blog posts from all over the internet
 4 October 2018
4 October 2018We look back at last year's Black Mathematician Month, and give a preview of what to expect this October.
 3 October 2018
3 October 2018You'll never believe number 3!
 27 September 2018
27 September 2018Join us at our upcoming launch party!
 20 September 2018
20 September 2018We explore the concept of emptiness in set theory, and explain how zero went from "nothing" to "something"
 6 September 2018
6 September 2018Introducing the work that has won mathematics' most famous award
 30 August 2018
30 August 2018Exploring the beauty of complex numbers, their origins and why they are important
 23 August 2018
23 August 2018How does one produce a net for the broadest class of polyhedra?
 16 August 2018
16 August 2018... and how Chalkdust played a role in one of them
 9 August 2018
9 August 2018Did you solve it?
 26 July 2018
26 July 2018Exploring non-random walks using fractions
 28 June 2018
28 June 2018A review of Vicky Neale's new book about the quest to understand prime numbers.
 21 June 2018
21 June 2018We analyse the maths and physics required to execute a good chip shot
 14 June 2018
14 June 2018Discover the mathematical equations that describe the most commonly observed trajectories in football
 7 June 2018
7 June 2018An unexpected way to beat the odds in this classic game
 4 June 2018
4 June 2018Defining what exactly an integral is leads naturally to an explanation of how to handle approximating them.
 31 May 2018
31 May 2018A selection of weird goings-on from the world of fluid mechanics
 17 May 2018
17 May 2018A thrilling review of this truly enlightening book
 10 May 2018
10 May 2018Blood is exceptionally complicated and its composition varies from person to person. So how do we begin to model it?
 3 May 2018
3 May 2018A mathematically-themed version of the classic card game, with several new features
 26 April 2018
26 April 2018A collection of our favourite and least favourite things named after Euler, from issue 07
 19 April 2018
19 April 2018Have you been wondering what the pattern on it means?
 12 April 2018
12 April 2018``Read Euler, read Euler, he is the master of us all." -- Laplace. An invitation to join us in celebrating Euler's 311th birthday by appreciating a few of his great contributions to mathematics.
 5 April 2018
5 April 2018Or, how a simple problem can get very complicated, very quickly...
 29 March 2018
29 March 2018Let's take a look at patterns that can be discovered in Fibonacci numbers and how we can find them around us.
 8 March 2018
8 March 2018You won't believe number 5!
 1 March 2018
1 March 2018What is the probability that d+2 random points in d-dimensional space form a convex body? Investigating an old problem using modern methods.
 26 February 2018
26 February 2018Join us at our upcoming launch party!
 23 February 2018
23 February 2018"Unlocking the hidden mathematics in video games"
 14 February 2018
14 February 2018Learn how to model your heart one beat at a time ❤️
 8 February 2018
8 February 2018Belgin plays a classic mathsy game from her childhood...in 16-bit graphics! Here's her review...
 1 February 2018
1 February 2018You can un-knot a knot, by cutting it not?
 25 January 2018
25 January 2018Why do surnames die out? We take a look at the Galton-Watson process for modelling the extinction of surnames to answer the question: 'When will we all be Smiths?'
 24 January 2018
24 January 2018Did you solve it?
 18 January 2018
18 January 2018A fiendish puzzle for you to 'pour' over...
 11 January 2018
11 January 2018Some summations seem strangely slippery...
 4 January 2018
4 January 2018Uniting the teaching of mathematics and music can benefit pupils greatly in both areas.
 31 December 2017
31 December 2017What have we been up to this year?
 31 December 2017
31 December 2017... and the winners
 22 December 2017
22 December 2017Can you solve four puzzles to reveal the hidden message?
 21 December 2017
21 December 2017Reviewing this week's conundrum prize... science-y stuff staring you in the face!
 18 December 2017
18 December 2017Try our nonograms! And remember, not all puzzles have a unique solution...
 14 December 2017
14 December 2017Christmas is coming, and Santa will soon begin his journey. We analyse the science and maths behind his trip.
 11 December 2017
11 December 2017Solve this and you could be the lucky winner of a signed copy of The Indisputable Existence of Santa Claus
 7 December 2017
7 December 2017We round up some of the last month's top mathematical posts from around the internet
 4 December 2017
4 December 2017Solve this and you could be the lucky winner of a Chalkdust T-shirt
 30 November 2017
30 November 2017As the festive season strikes again, we'll be dishing out more fiendish puzzles – this time with prizes!
 23 November 2017
23 November 2017Should you ask Santa for 'Ice Col' Beveridge's encyclopedic tome this festive period?
 16 November 2017
16 November 2017Chalkdust descends upon the UK's largest pop maths gathering and tells you what you missed
 9 November 2017
9 November 2017When you get tired of using your calculator for numbers, why not use it for words?
 2 November 2017
2 November 2017Maths has strong connections to art and music, but what about to both at the same time?
 31 October 2017
31 October 2017Reflecting on what we've learnt over the past few weeks.
 25 October 2017
25 October 2017Stories and lessons on diversity in mathematics from a globe-trotting number theorist.
 19 October 2017
19 October 2017Cardioids in coffee cups, counting with three fingers, and breakfast at Villani's. Plus the return of all your favourite fun pages in our autumn 2017 issue.
 17 October 2017
17 October 2017How many did you spot?
 6 October 2017
6 October 2017Natalya Silcott introduces us to star polynomials!
 2 October 2017
2 October 2017Promoting black mathematicians, and talking about building a more representative mathematical community.
 2 October 2017
2 October 2017Free launch party, 7.15pm. Come along!
 28 September 2017
28 September 2017A polygon with four and a half sides?!
 21 September 2017
21 September 2017While drinking beer in your favourite pub, have you ever wondered how it is produced? Find here some of the science and mathematics behind brewing.
 14 September 2017
14 September 2017Take a ball, divide it into parts, glue them back and get two identical copies of your ball!
 7 September 2017
7 September 2017A hideous equation that hides beautiful images, and much (much) more besides...
 31 August 2017
31 August 2017How processes used in image editing are related to mathematics!
 24 August 2017
24 August 2017We created hot ice from scratch, a solution that remains liquid even below its freezing point!
 17 August 2017
17 August 2017A quick look at how to get the most bang for your buck the next time you're in a bidding war
 10 August 2017
10 August 2017A summer essential or an embarrassment risk on the streets of Ibiza?
 3 August 2017
3 August 2017How to win a game when your expected score is 0
 27 July 2017
27 July 2017Did you win?
 20 July 2017
20 July 2017Write down a quadratic. What is the probability that it factorises? Paging Prof. Dirichet...
 13 July 2017
13 July 2017A crossnumber clue takes us plunging headfirst towards projective geometry
 11 July 2017
11 July 2017Human migration with mathematical models, data and a hands-on experiment!
 6 July 2017
6 July 2017Some interesting observations with the pigeonhole principle
 29 June 2017
29 June 2017Have a go at these puzzles, adequate for your holidays!
 22 June 2017
22 June 2017We take a look at the top 10 emojis!
 15 June 2017
15 June 2017Next time you are finished using a paper cup, create your own papercupter!
 8 June 2017
8 June 2017Read about our least favourite numbers in this collection from issue 5!
 1 June 2017
1 June 2017Discover the mysteries behind the most spectacular free-kick ever scored and how Newton can help us to simulate it.
 25 May 2017
25 May 2017Finding the best picture at the Leaning Tower of Pisa is all about the maths rather than the pose!
 17 May 2017
17 May 2017Each time you eat a croissant you might be biting more than 500 layers of dough!
 11 May 2017
11 May 2017We have a go at the puzzles in Daniel Griller's new book
 4 May 2017
4 May 2017We chat to Marcus about science communication, teaching mathematics in schools, and how to make group theory sound sexy.
 27 April 2017
27 April 2017Negative polygons and other mathematical creations
 20 April 2017
20 April 2017In the Aztec city of Atzlan, the scientist Remotep makes a revolutionary discovery
 16 April 2017
16 April 2017How optimising the space around a circular monument is related to supereggs
 13 April 2017
13 April 2017When you're caught in the rain without an umbrella... what is your best option?
 6 April 2017
6 April 2017Unexpected item in bagging areAAAARGGGHH here's 90p change in pennies
 30 March 2017
30 March 2017After 100 years, a key postulate of the third law of thermodynamics has been proven. We meet Lluis Masanes, one of the researchers responsible.
 27 March 2017
27 March 2017Not the new coin we want, but the new coin we need
 23 March 2017
23 March 2017How to make the most slices from just a few cuts of cake
 6 March 2017
6 March 2017Graphical linear algebra, slide rules and game theory in nature. Plus all your favourite fun pages in our spring 2017 issue.
 2 March 2017
2 March 2017How many did you spot?
 23 February 2017
23 February 2017Free launch party, 7.15pm. Come along! Free copies of Chalkdust, free pizza, and buy your own Chalkdust T-shirt.
 16 February 2017
16 February 2017What connects the products of twin primes with something you learnt in primary school and the number 8?
 14 February 2017
14 February 2017A tragic love story of shares and viral songs. To share, or not to share...
 9 February 2017
9 February 2017For those of you tackling this dilemma, here's your answer...
 2 February 2017
2 February 2017Some surprising mathematical facts
 27 January 2017
27 January 2017Here are some highlights of the first two years of Chalkdust!
 26 January 2017
26 January 2017Are you a winner?
 19 January 2017
19 January 2017Lindsay Lohan is really good at L'Hôpital's rule.
 12 January 2017
12 January 2017Why the infamous acronym needs revising.
 5 January 2017
5 January 2017Can you wear them and be taken mathematically seriously?
 22 December 2016
22 December 2016Behind today's door... A book review!
 15 December 2016
15 December 2016This year's Chalkdust puzzle Christmas card
 8 December 2016
8 December 2016Winter is coming!
 1 December 2016
1 December 2016Get into the ChristMATHS spirit with the maths behind the popular Christmas carol!
 24 November 2016
24 November 2016How crime science, and the maths it uses, is helping the police fight crime
 17 November 2016
17 November 2016Here we have collected our favourite sets, from the Mandelbrot set to the Mahut-Isner set!
 10 November 2016
10 November 2016Using modern technology to understand geometry
 3 November 2016
3 November 2016The algebra will set your heart aflutter.
 27 October 2016
27 October 2016Constructing a spiderweb: in the spookiest and most horrific way possible!
 20 October 2016
20 October 2016The Great Fire of London, a little-known polymath and a Monument...
 13 October 2016
13 October 2016A blast from the past. Modelling battle grounds from ancient Greece.
 2 October 2016
2 October 2016Tuesday 11 October, 7.15pm. Come along! Featuring hundreds of free copies of Chalkdust, free pizza, and the chance to purchase a Chalkdust T-shirt.
 29 September 2016
29 September 2016A review of Timothy Revell's new book, describing the hidden mathematics behind our world
 15 September 2016
15 September 2016If only the Earth were flat...
 8 September 2016
8 September 2016Applying game theory to evolution
 2 September 2016
2 September 2016What can a 100-year-old result in topology say about weather and computers?
 25 August 2016
25 August 2016Donald Duck learns that there is “a lot more to mathematics than two-times-two”.
 18 August 2016
18 August 2016Exploring the maths on offer at this year's UK hacker festival.
 11 August 2016
11 August 2016How the queue size tells you when the next bus is coming
 4 August 2016
4 August 2016Believe it or not: Mathematics and Theology can coexist
 28 July 2016
28 July 2016Are you a winner?
 21 July 2016
21 July 2016Looking for a neat description of this useful matrix part-inverse
 14 July 2016
14 July 2016Can you solve these puzzles about differentiation and integration?
 7 July 2016
7 July 2016Difficulties in designing a voting system for referenda
 30 June 2016
30 June 2016Using Markov chains to calculate some interesting tennis stats!
 23 June 2016
23 June 2016Paper cups do not follow a hexagonal pattern and the cones do not meet at a single point, but they do make a gigantic sphere
 9 June 2016
9 June 2016Memory and maths in the modern world
 2 June 2016
2 June 2016An easy equation to remember for your driving theory test, with dangerous consequences
 26 May 2016
26 May 2016The discovery of gravitational waves offers a new way of looking at the universe. Who knows what we will discover?
 19 May 2016
19 May 2016The Chalkdust team set you a challenge, for which the prize is a £25 Amazon voucher...
 12 May 2016
12 May 2016Extending the million, billion, trillion system to much, much bigger numbers
 5 May 2016
5 May 2016Maths and Decision Theory to be the best at playing Guess Who?
 28 April 2016
28 April 2016When-to-add-milk confusion and other related matters
 21 April 2016
21 April 2016The search for polydivisible numbers in different bases: how many can you find?
 14 April 2016
14 April 2016This month's round up of mathematical blog posts.
 7 April 2016
7 April 2016Here is the reason why the golden era of Twitter is gone
 31 March 2016
31 March 2016Hyperbolic surfaces, Klein bottles and more
 24 March 2016
24 March 2016Read ours then send us your favourites!
 17 March 2016
17 March 2016How many points could you have scored at our launch quiz?
 3 March 2016
3 March 2016Explaining how surface tension makes water form surprising shapes
 25 February 2016
25 February 2016Your first peek at our Spring issue
 18 February 2016
18 February 2016Additional roads do not imply faster travel times!
 11 February 2016
11 February 2016Agony uncle Professor Dirichlet answers your personal problems this Valentine's Day.
 11 February 2016
11 February 2016Make the perfect gift for your loved one
 4 February 2016
4 February 2016How can we identify objects in photos, to diagnose cancer or predict the weather? Using gradients!
 28 January 2016
28 January 2016Simple Statistics can help businesses make informed decisions
 21 January 2016
21 January 2016Introducing polyominoes
 19 January 2016
19 January 2016Amaze your friends with our top facts about the new largest known prime number
 14 January 2016
14 January 2016Is there life on Mars? Or anywhere else?
 7 January 2016
7 January 2016Exploring mental arithmetic tricks in T. Martin's 1842 guide, 'Pounds, shillings and pence'
 31 December 2015
31 December 2015Have you read the best of the blog?
 24 December 2015
24 December 2015Something for you to solve during the post-Christmas lull
 17 December 2015
17 December 2015Agony uncle Professor Dirichlet answers your personal problems this Christmastime.
 10 December 2015
10 December 2015Are you a winner?
 3 December 2015
3 December 2015Making gingerbread Platonic solids, Fröbel stars and Christmas flexagons
 26 November 2015
26 November 2015We have received loads of feedback from people telling us their favourite function
 19 November 2015
19 November 2015Three ways to obtain and generalise a beautiful fractal
 12 November 2015
12 November 2015Chalkdust visits popular maths' biggest conference
 5 November 2015
5 November 2015Explaining the tautological Twitter bot
 29 October 2015
29 October 2015Because we love functions!
 22 October 2015
22 October 2015Where should you choose to take a conversion kick from?
 15 October 2015
15 October 2015Some mathematical questions you might have wondered every time you look at one of those rainbows
 8 October 2015
8 October 2015What difference will an extra 10 balls make?
 1 October 2015
1 October 2015Take two phone books and interleave all their pages one by one. Now try and pull them apart by their spines. Impossible, right?
 24 September 2015
24 September 2015Find out what's going to be inside
 17 September 2015
17 September 2015Maths on Toast is a charity that aims to challenge and change the public's perception of mathematics...
 10 September 2015
10 September 2015A selection of our favourite mathematical blogs
 3 September 2015
3 September 2015While we work on issue 2
 27 August 2015
27 August 2015The extreme weirdness of slow viscous flows, and why borrowers shouldn't use doggy paddle.
 20 August 2015
20 August 2015Can you solve our 3D Sudoku puzzles?
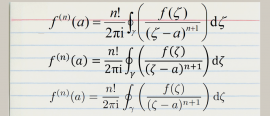 13 August 2015
13 August 2015Let's print your thesis in Comic Sans
 6 August 2015
6 August 2015Do we have a natural limitation on the number of friends that we have?
 30 July 2015
30 July 2015Are you a winner?
 23 July 2015
23 July 2015Did you use meta-logic to solve the crossnumber?
 16 July 2015
16 July 2015How to make Sudoku more interesting
 9 July 2015
9 July 2015Why are there none in base 13?
 3 July 2015
3 July 2015What the Guardian got wrong...
 2 July 2015
2 July 2015How tennis players spin and slice their serves
 25 June 2015
25 June 2015Favourite numbers for many are linked to birthdays or anniversaries, but here is our take on the question
 18 June 2015
18 June 2015When people do science for money…
 11 June 2015
11 June 2015If you enjoyed Hannah's sweets then you'll love these...
 4 June 2015
4 June 2015Choosing which charity we donate money to shouldn't be an entirely emotional decision.
 28 May 2015
28 May 2015Cédric Villani’s Birth of a Theorem tells the story of a mathematical theorem
 21 May 2015
21 May 2015Does form going into the play-offs predict your success?
 14 May 2015
14 May 2015Pub ✕ maths = ?
 7 May 2015
7 May 2015What does Twitter have to do with politics?
 30 April 2015
30 April 2015We have some fantastic blog articles, and this is how we plan to publish them.